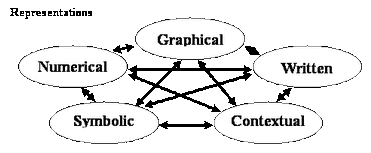
Goals and Lessons -> Cross-discipline Instruction
Using the ideas outlined below, I hope to:
- Create a classroom where multiple languages and cultures are valued, respected, and incorporated.
- Provide classroom experience in real-world mathematics for students.
- Learn from other students how mathematical and ELA concepts function in their lives.
- Make explicit the ways in which mathematics and ELA instruction connects to the everyday lives of other students.
- Create a community where critical thinking, social awareness, and respect are expectations of everyone in the classroom.
Mathematics Symbolic System as Language
As a future mathematics teacher (hopefully), I aim to integrate Language Arts skills into my mathematics classroom. One of the ways I've thought about this goal is to treat math as a language. In his article "Math as a Second Language" Professor Dara V. Wakefield in Curriculum and Instruction at Berry College outlines the ways in which math is like a language:
• Abstractions (verbal or written symbols representing ideas or images) are used to communicate.
• Symbols and rules are uniform and consistent.
• Expressions are linear and serial.
• Understanding increases with practice.
• Success requires memorization of symbols and rules.
• Translations and interpretations are required for novice learners.
• Meaning is influenced by symbol order.
• Communication requires encoding and decoding.
• Intuition, insightfulness, and "speaking without thinking" accompany fluency.
• Experiences from childhood supply the foundation for future development.
• The possibilities for expressions are infinite.
(Wakefield, 2012)
It is my goal to pursue ways in which I can create a classroom students can combine skills from Language Arts, and other subjects, to help them learn mathematical concepts and skills. Because mathematics uses similar ways of approaching problems, concepts, and processes as second language learning, I find it important to incorporate language into my future mathematics classroom.
• Abstractions (verbal or written symbols representing ideas or images) are used to communicate.
• Symbols and rules are uniform and consistent.
• Expressions are linear and serial.
• Understanding increases with practice.
• Success requires memorization of symbols and rules.
• Translations and interpretations are required for novice learners.
• Meaning is influenced by symbol order.
• Communication requires encoding and decoding.
• Intuition, insightfulness, and "speaking without thinking" accompany fluency.
• Experiences from childhood supply the foundation for future development.
• The possibilities for expressions are infinite.
(Wakefield, 2012)
It is my goal to pursue ways in which I can create a classroom students can combine skills from Language Arts, and other subjects, to help them learn mathematical concepts and skills. Because mathematics uses similar ways of approaching problems, concepts, and processes as second language learning, I find it important to incorporate language into my future mathematics classroom.
Specific Skill Set #1

Proving - Inferencing - Predicting - Patterns
Predictions and generalizing patterns requires an application of inferencing, “the ability to connect what is in the text with what is in the mind to create an educated guess.” (Beers, 2003). Once basic rules are mastered, students must generalize from specific examples to provide a rules for some mathematical situation. At the purest mathematical level, mathematicians attempt to take known rules to conclude new rules never before conceived or proved.
As students learn how to predict what might happen in a text, they are applying patterns they've seen within the text and among texts in general. In math, solving problems out of the context of a specific section of a textbook often rests on figuring out which pattern the problem falls into. Also, in order to create a mathematically rigorous proof, students must learn how to logically connect each statement with the next based on a set of given rules, which is analogous to how students of English are taught to inference from a text or write an essay, which, in itself, is a proof of one’s inferences. Explicating the results of inferencing itself is exactly what pure mathematics is all about, with a more precise form of inferencing being that ever present ‘show your work’ on math tests from elementary school through college.
Predictions and generalizing patterns requires an application of inferencing, “the ability to connect what is in the text with what is in the mind to create an educated guess.” (Beers, 2003). Once basic rules are mastered, students must generalize from specific examples to provide a rules for some mathematical situation. At the purest mathematical level, mathematicians attempt to take known rules to conclude new rules never before conceived or proved.
As students learn how to predict what might happen in a text, they are applying patterns they've seen within the text and among texts in general. In math, solving problems out of the context of a specific section of a textbook often rests on figuring out which pattern the problem falls into. Also, in order to create a mathematically rigorous proof, students must learn how to logically connect each statement with the next based on a set of given rules, which is analogous to how students of English are taught to inference from a text or write an essay, which, in itself, is a proof of one’s inferences. Explicating the results of inferencing itself is exactly what pure mathematics is all about, with a more precise form of inferencing being that ever present ‘show your work’ on math tests from elementary school through college.
Specific Skill Set #2
Graphing - Visualizing
When students are taught or told to visualize a text they are reading, they are expected to create a sense image, using as many senses as possible, showing themselves what the text might look like if it were a movie or an experience they themselves were having. Similarly, when mathematics students are taught how to graph equations or solve word problems, they are being asked to picture what these symbols are ‘actually’ saying.
When students are taught or told to visualize a text they are reading, they are expected to create a sense image, using as many senses as possible, showing themselves what the text might look like if it were a movie or an experience they themselves were having. Similarly, when mathematics students are taught how to graph equations or solve word problems, they are being asked to picture what these symbols are ‘actually’ saying.
Modalities in the Classroom
It's impossible to be a mathematician without being a poet in soul.
What do I mean by modalities?
What does using different modalities do for students, teachers, and the classroom?
Examples in the (math) classroom: *For more in-depth lessons, see lesson plans.
- Ways in which information is presented, encoded, and represented.
- Sensory pathways through which students receive, store, and give information.
- Media, popular culture, learning 'styles' of students
What does using different modalities do for students, teachers, and the classroom?
- Opens curriculum to students' lived experiences.
- Allows for multiple viewpoints to be expressed and valued in the classroom.
- Opens dialogue within classroom about greater world.
Examples in the (math) classroom: *For more in-depth lessons, see lesson plans.
- Using poetry to explain mathematical concepts. (Example)
- Re-writing math problems in English, or word problems in math. (i.e. 'diagramming' mathematical sentences)
- Asking students to bring in something related to the concepts in the unit. (i.e. in a graphing unit having students bring in examples of comparisons in their lives or keep track of the types of things they use in order to create a word problem for graphing practice)
- Use mathematics to help explore English concepts. (Such as using and understanding statistics to help understand evidence and backing in argument writing).